Merge Sort in Java
0 CommentsLast Updated on May 25, 2019 by Simanta
In this post, I will explain the Merge Sort algorithm and how to use it in Java.
Sorting is the process of arranging data in ascending or descending order. Sorting becomes necessary while searching a particular record in database, a particular telephone number in telephone directory, words in a dictionary, and so on.
In computer applications, sorting is a common operation, and there are several efficient algorithms to sort data. One such popular sorting algorithm is Merge Sort.
The Merge Sort Algorithm
Merge sort is basically a Divide and Conquer algorithm to sort a given set of elements recursively and then merge them. This algorithm runs in O(n*log n) time in all cases, where n is the number of comparisons done.
Merge sort uses not-in-place sorting. In this type of sorting, the algorithm requires extra space for comparison and temporary storage of data elements. Therefore, for merge-sort, the required space is more than or equal to the elements being sorted. This is one of the drawback of Merge sort. However, with the cost of resources getting lesser, not-in-place sorting should not be a concern unless you are going for some extremely big data computation in an environment with limited resource.
To sort data, Merge Sort performs the following steps:
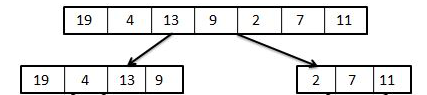
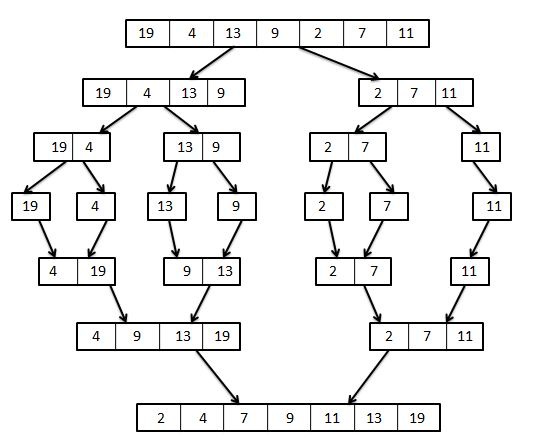
- It splits the items in the collection into two collections. To do so, it takes the middle of the collection and split the collection into its left and its right part, like this.
- The resulting collections are again split recursively until they are broke to a single item in each collection.
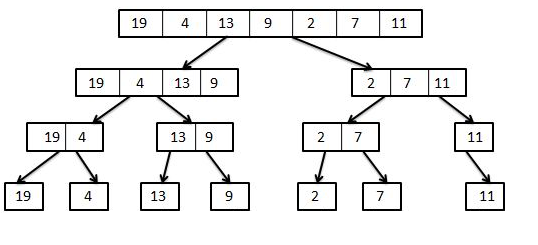
As you can see in this Figure, now we have single item in all the sub collections. At this point, we can say that, since each collection has only one item in it, everything is sorted.
- Next, Merge sort starts merging the collections. The step of merging involves comparing two sub collections, and then appending the larger one to the end of the smaller one. This goes on, until we end up with one single, sorted collection.
When we were dividing, we were doubling the number of collections until we reached our base case of one item per collection.
Now, we’re doing the exact opposite in order to build our collection up.
This figure shows the complete process of Merge sort.
Implementing Merge Sort
An example of implementing Merge sort in Java is this.
MergeSortExample.java
package springframework.guru.mergesort.mergesortexample;
public class MergeSortExample {
public Comparable[] mergeSort(Comparable[] inputList) {
if(inputList.length <= 1) {
return inputList;
}
Comparable[] list1 = new Comparable[inputList.length/2];
Comparable[] list2 = new Comparable[inputList.length - list1.length];
System.arraycopy(inputList, 0, list1, 0, list1.length);
System.arraycopy(inputList, list1.length, list2, 0, list2.length);
mergeSort(list1);
mergeSort(list2);
merge(list1, list2, inputList);
return inputList;
}
public void merge(Comparable[] list1, Comparable[] list2, Comparable[] resultList) {
int indexOfList1 = 0;
int indexOfList2 = 0;
int indexOfMergedList = 0;
while(indexOfList1 < list1.length && indexOfList2 < list2.length) {
if(list1[indexOfList1].compareTo(list2[indexOfList2]) < 0) {
resultList[indexOfMergedList] = list1[indexOfList1];
indexOfList1++;
}else {
resultList[indexOfMergedList] = list2[indexOfList2];
indexOfList2++;
}
indexOfMergedList++;
}
System.arraycopy(list1, indexOfList1, resultList, indexOfMergedList, list1.length - indexOfList1);
System.arraycopy(list2, indexOfList2, resultList, indexOfMergedList, list2.length - indexOfList2);
}
}
In this code, the mergeSort() method takes an array to sort as input. If the input array has a single element, there is no need of sorting and the method just returns back the input array.
If the array has more than one element, the method splits the array into two halves, and sorts the splitted arrays recursively. The code then calls the merge() method to merge the sorted array.
I’ve written a JUnit test to test the sorting function. If you are new to JUnit, I suggest going through my Junit series.
The MergeSortExampleTest class is this.
MergeSortExampleTest.java
package springframework.guru.mergesort.mergesortexample;
import org.junit.After;
import org.junit.Before;
import org.junit.Test;
import java.util.Arrays;
import static org.assertj.core.api.Assertions.assertThat;
public class MergeSortExampleTest {
MergeSortExample mergeSortExample;
Integer[] arrayOfElements = {19, 4, 13, 9, 2, 7, 11};
@Before
public void setUp() {
mergeSortExample = new MergeSortExample();
}
@After
public void tearDown() {
mergeSortExample = null;
}
@Test
public void mergeSortTest() {
System.out.println("Array before sorting: " + Arrays.toString(arrayOfElements));
mergeSortExample.mergeSort(arrayOfElements);
System.out.println("Sorted array is: " + Arrays.toString(arrayOfElements));
assertThat(arrayOfElements).containsExactly(2, 4, 7, 9, 11, 13, 19);
}
}
The output on running the test in IntelliJ is this.

Summary
Merge sort is not the only algorithm for sorting data. Other sorting algorithms includes insertion sort, bubble sort, quicksort, and heap sort.
I won’t go into the details of comparing them in this post. I will leave you with few pointers on when to use Merge sort.
- Merge sort requires additional storage proportional to the number of records to be sorted. Therefore, if data is in a list-like structure and storage is available, merge sort is a superior algorithm.
- Merge sort is very efficient for immutable data structures like linked lists since linked list elements are scattered throughout memory. Using Merge sort makes it easy for sorting as it makes only fewer total comparisons. Also, pointers can easily be changed when merging.
- Merge sort is well suited in multithreaded programming. So if you have to sort very large data sets with possible parallelization, Merge sort is the algorithm to go for.